Fotometría PSF

Desde el punto de vista astronómico, la Fotometría es la medición, calculo y cuantificación de la luz emitida por diferentes objetos astronómicos. Etimilogicamente, proviene de la voz griega “φωτος” (photos,luz) y del sufijo “μετρια” (metria, medida).

De esta forma, la fotometría es la medición del flujo integrados $F$ (cuentas/tiempo x area) de una fuente en el cielo, y se define matemáticamente de la siguiente forma:

Donde $F_{\lambda}$ es el flujo específico proveniente de la fuente, y $S_{\lambda}$ la función de transmisión, que toma en cuenta la respuesta del detector, la condiciones atmosféricas y el filtro que se ha usado. Lógicamente, y por cómo está planteada la medición, mientras mayor sea el tiempo $t$, mayor flujo integrado se obtiene.

Magnitudes y flujos

La magnitud astronómica es, por definición, una cantidad relativa. Esto quiere decir que su valor es definido con respecto a una fuente específica (como por ejemplo, el sistema fotométrico basado en la estrellas Vega). Dos variaciones populares de la magnitud astronomómica son las siguientes:

• Magnitud Bolométrica: $$ \displaystyle m_1 - m_2 = 2.5\log_{10}\left(\frac{F_2}{F_1}\right) $$

• Magnitud específica: $$ m_{\lambda,1} - m_{\lambda,2} = 2.5\log_{10}\left(\frac{F_{\lambda,2}}{F_{\lambda,1}}\right) $$

Entonce, necesitamos los Flujos de, al menos, dos estrellas relativamente cercana. Hay tres métodos principales para medir dicho flujo $F$:

1. Fotometría de apertura.
2. Fotometría diferencial.
3. Fotometría de función de dispersión de punto, o point-spread-function (PSF).

Cada una de estas técnicas posee diferentes filosofías, ventajas y desventas, pero todos tienen en común algunos parámetros. Partamos con la primera:

Fotometría de apertura

Esta técnica se basa en considerar todas las cuentas (ADU) dentro de un radio $R$ definido, el cual es llamado "apertura", teniendo como regla que el radio de apertura debe ser, a lo menos, menor que el seeing $R<seeing$ (visión o visibilidad astronómica).

Hay que recordar que una imagen (astronómica, fotográfica, etc) es un arreglo de datos de $(n \times n)$ píxeles, entonces los valores $I_{ij}$ describiran las coordenadas físicas de la imagen. Naturalmente, el flujo de luz proveniente de una fuente estelar, por un tiempo de antemano conocido, puede ser estimado sumando cada pixel $I_{ij}$ dentro de la circunferencia caracterizada por el radio R. En palabras más precisas, dentro de la apertura.

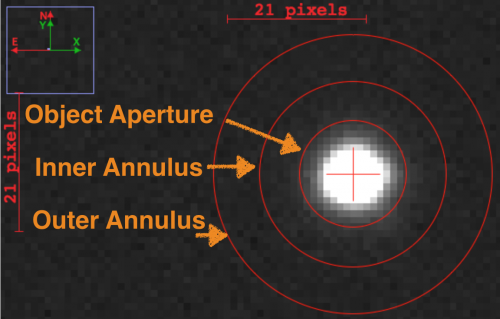
Luego, debemos sustraer la contribución del cielo a la medición usando alguna estimación directa del valor de "cielo". Podemos pensar en esta contribución como el ruido de fondo de la imagen, y será cuantificado como el valor promedio de una imagen en lugares donde no existen objetos astronómicos. Para estimar el cielo, se define una región llamada "Annulus", que es una estructura creada con dos circulos que posee forma de donut. La idea es medir la contribución local (el área circundante) de la imagen para obtener el flujo usando algún estadístico, digamos, el promedio.

La Figura 1 representa de mejor manera este concepto. Por ejemplo, medimos todos los píxeles $I_{ij}$ dentro del radio interior (Inner Annulus marcado en la imagen) y el exterior (Outer Annulus), obtenemos un valor promedio y será considerado el cielo.

Bajo esta interpretación, el número total de cuentas $I$ dentro del radio de apertura $R$ será la suma de cada uno de los píxeles $I_{ij}$ de la imagen dentro del radio R considerado, menos la contribución del cielo $I_{cielo}$ en cada píxel:

donde:

1. $I$: Cuentas totales de la fuente dentro del radio de apertura.
2. $I_{ij}$: Cuentas específicas en cada pixel dentro del radio de apertura.
3. $n_{pixeles}$: Número de píxeles dentro de la apertura.
4. $I_{cielo}$: Valor de la contribución estimada del cielo usando el annulus. Usualmente es llamado 'Cielo'.

Generalmente, el valor del cielo se obtiene desde la distribución del número de cuentas dentro de la imagen.

Finalmente, la magnitud instrumental viene dado por:

El termino constante depende de las variables asociadas a las condiciones de observación (por ejemplo la extincion atmosferica, la masa de aire, el seeing), y básicamente es lo que se modifica para poder calibrar la fotometría en cierca escala de interés.

La gran desventaja de este método es la alta densidad estelar. No es posible usar fotometría de apertura cuando la fuente bajo estudio no está aislada, que es el caso de grupos de estrellas como los Cúmulos globulares, o en el centro de nuestra galaxia. De alguna forma, el veloz avance de la resolución espacial de las nuevas generaciones de telescopios ha demostrado que la fotometría de apertura es la primera aproximación a la medición del flujo estelar (o gáctico).

Fotometría Diferencial

La fotometría diferencial consiste en usar estrellas de comparación dentro de la misma imagen para estudiar una estrella en particular, y así ignorar hasta cierto punto las variables atmosféricas y el tiempo de integración. Este método está enfocado en cuantificar la variabilidad estelar de la fuente de interés, y para ser implementada es necesario elegir unas 4 o 10 estrellas de comparación C, medir su magnitud instrumental $m_C$ a través de varias observaciones (o épocas) y calcular el diferencial de magnitud $\Delta m_C$ de cada estrela de comparación, con el fin de cuantificar el cambio de brillo de la estrella de interés.

Este método ofrece muy buenos resultados cuando la cadencia de observación es alta, siendo uno de los favoritos del AAVSO, Kepler, entre otros, pero desconozco si es un método que se siga usando de forma masiva, pero es una interesante forma de medir la luz de las estrellas.

Fotometría PSF

Este método se basa en la idea que todas las fuentes en una imagen tienen exactamente la misma forma. En otras palabras, la distribución espacial de la luz capturada sobre una imagen sigue alguna regla general, que puede ser usada para estimar el flujo F.

PSF es un acrónimo en ingles Point spread functionLa aproximación más usual es asumir que las fuentes poseen un perfil Gaussiano con la misma desviación estándar. Con esta aproximación, el "tamaño" o apertura para una fuente estará caracterizada por el seeing atmosférico. Dependiendo del tamaño de la imagen en la cual trabajemos, podemos considerar que tenemos, en promedio, las mismas perturbaciones atmosféricas. Bajo estas consideraciones, todas las estrellas deberían ser descritas por la misma función puntual de dispersión (point spread function, PSF).

La forma radial de una Gaussiana bidimensional se describe como:

donde:

1. $I(r)$ Es la intensidad para algún pixel de coordenadas $(x,y)$.
2. $r=\sqrt{x^2+y^2}$ es la componente radial de una Gaussiana 2-D.
3. $I_{0}$ Es el peak de intensidad del perfil.
4. $\sigma$ Es la desviación estándar del perfil (el ancho del perfil Gaussiano).

La simpleza y utilidad de la fotometría PSF recae en que todas las estrellas pueden ser modeladas usando, en este caso, un perfil Gaussiano con la misma desviación estándar (seeing) $\sigma$, y cada una con diferentes intensidades $I_0$, lo que reduce el problema a elegir un set de parámetros para cada imagen a analizar.

A continuación, se presentan 3 estrellas de diferentes magnitudes, pero que presentan la misma forma:

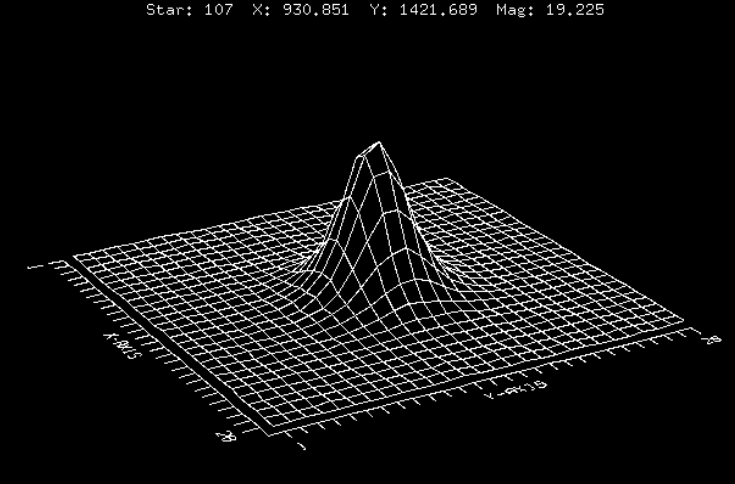
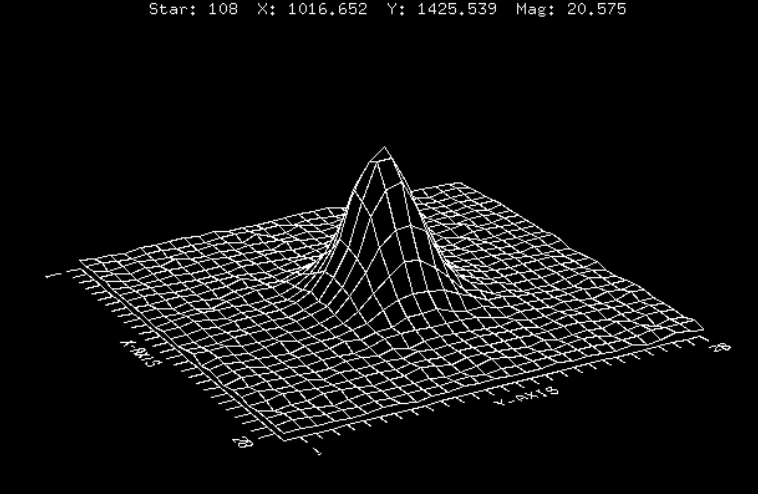
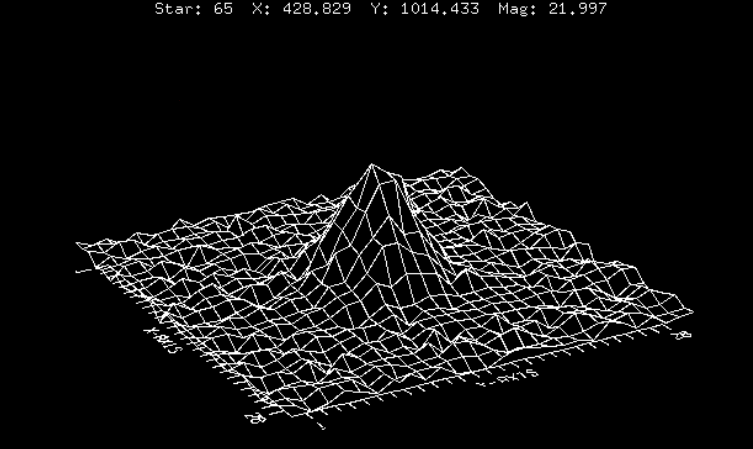
¿Cuál es la diferencia? La forma de la fuente se mantiene, pero el nivel de ruido del fondo crece. En general, si el peak de intensidad $I_0$ está por sobre el límite del ruido, podrá ser detectada y analizada.

Para entender mejor la idea, simularemos una estrella usando una distribución gaussiana y estudiaremos sus parámetros con más detalles. Le añadiremos ruido para hacer todo un poco más realista.

#Agregamos las librerias fundamentales para trabajar.
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import os
import sys

#Creamos el dominio:
Rango_imagen=100
numero_filas    = 100
numero_columnas = 100

x   = np.linspace(-Rango_imagen, Rango_imagen, numero_columnas)
y   = np.linspace(-Rango_imagen, Rango_imagen, numero_filas)
X,Y = np.meshgrid(x, y)

#calculo de la intensidad
r0 = 0                                    #Desplazamiento
sigma = 20.                               #Desviación estándar.
I0= 1000.                                 #Peack de intensidad.
R = np.sqrt((X-r0)**2 + (Y-r0)**2)        #Componente radial.

#Calculamos el Perfil.
Perfil = I0*np.exp(-0.5*(R/sigma)**2)     

#Simulamos ruido que emule la contribución de fondo:
Valor_piso = 100.
desviacion_estandar_ruido = 150
Dimension_imagen = Perfil.shape
background = np.random.normal(Valor_piso, desviacion_estandar_ruido, Dimension_imagen)

#componemos todo:
Perfil_ruido = Perfil + background

#Hacemos el plot:
plt.figure(figsize=(12,6))

plt.subplot(121)
plt.title('Perfil Gaussiano')
plt.imshow(Perfil, cmap=cm.jet)
plt.colorbar(orientation='vertical', fraction=0.046) 
plt.xlabel('pixel X',fontsize=15)
plt.ylabel('pixel Y',fontsize=15)

plt.subplot(122)
plt.title('Perfil Gaussiano con ruido')
plt.imshow(Perfil_ruido, cmap=cm.jet)
cbar = plt.colorbar(orientation='vertical', fraction=0.046) 
cbar.ax.get_yaxis().labelpad = 20
cbar.ax.set_ylabel('Intensidad $I_0$', rotation=270, fontsize=15)
plt.xlabel('pixel X',fontsize=15)
plt.show()

#Creamos dos perfiles con la misma desviación estándar y diferente intensidad:
centro_imagen = len(X[:,0])/2

I1 = I0
I2 = 2700.                          #Peack de intensidad.

#Creamos un segundo perfil para comparar:
Perfil_2 = I2*np.exp(-0.5*(R/sigma)**2)     

#Simulamos (otro) ruido que emule la contribución de fondo:
background = np.random.normal(Valor_piso, desviacion_estandar_ruido, Dimension_imagen)

#componemos el segundo perfil:
Perfil_ruido_2 = Perfil_2 + background

plt.figure(figsize=(10,7))
plt.plot(X[centro_imagen],Perfil_ruido[centro_imagen],'ro',ms=7,label='$I_1 = %1.0f$' %I1)
plt.plot(X[centro_imagen],Perfil_ruido_2[centro_imagen],'kH',ms=6,label='$I_2 = %1.0f$' %I2)
plt.xlabel('pixel X',fontsize=15)
plt.ylabel(r'Intensidad',fontsize=15)
plt.plot([min(X[centro_imagen]),max(X[centro_imagen])], Valor_piso*np.ones(2),'g-',lw=4,label="Piso constante")
plt.legend(fontsize=15)
plt.show()

#Importamos todas las librerías necesarias para nuestro propósito:
from photutils.detection import IRAFStarFinder
from photutils.psf import IntegratedGaussianPRF, DAOGroup
from photutils.background import MMMBackground, MADStdBackgroundRMS
from astropy.modeling.fitting import LevMarLSQFitter
from astropy.stats import gaussian_sigma_to_fwhm

from astropy.table import Table
from photutils.datasets import (make_random_gaussians_table,
                                make_noise_image,
                                make_gaussian_sources_image)

#Ajustamos algunos valores para empezar
sigma_psf = 3.0
tshape = (32, 32)   #Dimensiones de la imagen

sources = Table()   #crea una tabla para mapear los parametros de 3 fuentes
sources['flux'] = [700, 1900, 1000]
sources['x_mean'] = [14, 16, 16]
sources['y_mean'] = [15, 15, 17]
sources['x_stddev'] = sigma_psf*np.ones(3)
sources['y_stddev'] = sources['x_stddev']
sources['theta'] = [0, 0, 0]
sources['id'] = [1, 2, 4]

#Crea la imagen, que será la suma de 3 fuentes, 
#y agregando ruido basado en una distribución de Poisson
# y ruido normal:
image = (make_gaussian_sources_image(tshape, sources) +
         make_noise_image(tshape, type='poisson', mean=8.,
                          random_state=1) +
         make_noise_image(tshape, type='gaussian', mean=0.,
                          stddev=5., random_state=1))

#ploteamos la imagen resultante:
plt.figure(figsize=(5,6))
plt.imshow(image, cmap='viridis', aspect=1, interpolation='nearest') 
plt.title('Imagen simulada') 
plt.colorbar(orientation='vertical', fraction=0.046, pad=0.04) 
plt.show()

#importamos más funciones especificas:
from photutils.detection import IRAFStarFinder
from photutils.psf import IntegratedGaussianPRF, DAOGroup
from photutils.background import MMMBackground, MADStdBackgroundRMS
from astropy.modeling.fitting import LevMarLSQFitter
from astropy.stats import gaussian_sigma_to_fwhm
from photutils.psf import IterativelySubtractedPSFPhotometry

#Medimos el cielo usando el estadistico MAD:
bkgrms = MADStdBackgroundRMS()
#usamos la imagen creada como dato de entrada:
std = bkgrms(image)

#Método para encontrar iterativamente fuentes en la imagen.
iraffind  = IRAFStarFinder(threshold=3.5*std, \
            fwhm=sigma_psf*gaussian_sigma_to_fwhm, \
            minsep_fwhm=0.01, roundhi=5.0, roundlo=-5.0, \
            sharplo=0.0, sharphi=2.0)

daogroup = DAOGroup(2.0*sigma_psf*gaussian_sigma_to_fwhm)

#estimamos la contribucion del cielo (background):
mmm_bkg = MMMBackground()

#eligen el modelo PSF:
psf_model = IntegratedGaussianPRF(sigma=sigma_psf)

#Creamos el modelo a aplicar en nuestra imagen:
photometry = IterativelySubtractedPSFPhotometry(finder=iraffind,
                                                group_maker=daogroup,
                                                bkg_estimator=mmm_bkg,
                                                psf_model=psf_model,
                                                niters=1, fitshape=(11,11))
#Realizamos la fotometría:
resultados = photometry(image=image)

#revisamos los parámetros principales de la fotometría, el flujo:
list(result_tab)

[<Row index=0 masked=True>
       flux_0            x_fit               x_0               y_fit               y_0              flux_fit        id  group_id      flux_unc           x_0_unc             y_0_unc       iter_detected
      float64           float64            float64            float64            float64            float64       int64  int64        float64            float64             float64           int32    
 ----------------- ------------------ ------------------ ------------------ ------------------ ------------------ ----- -------- ----------------- ------------------- ------------------- -------------
 2320.577813609559 15.489564216228956 15.531749294180742 15.775939905519783 15.318938753350247 2451.8336398655583     1        1 37.86912299152522 0.06859803592598557 0.06901161861692053             1]

#obtenemos la imagen residual de la ejecución anterior.
residual_image = photometry.get_residual_image()

plt.figure(figsize=(9,6))

plt.subplot(121)
plt.imshow(image, cmap='viridis', aspect=1, interpolation='nearest')
plt.title('Imagen simulada')

plt.subplot(122)
plt.imshow(residual_image, cmap='viridis', aspect=1,
           interpolation='nearest', origin='lower')
plt.title('Imagen residual')
plt.show()