Estimado estudiantado,
Es de mi agrado informar que este espacio será exclusivo para desarrollar ideas, ordenar reflexiones, realizar cálculos y brindar información sobre el actual curso de “Física de fronteras”, donde estudiaremos los fenómenos físicos de vanguardia en los últimos 100 años.
Algunos cálculos que quizá no son vitales para el entendimiento de este curso, serán desarrollados en este espacio con el fin de que ustedes puedan verlos y sabes desde dónde provienen las ideas contra-intuitivas de la realidad.
Las diapositivas actualizadas (hasta el 03/04/24) se encuentran en ESTE LINK!
Conceptos previos
Cualquier persona que ha manipulado una expresión matemática alguna vez en su vida debe haber notado que estas pueden tomar longuitudes inesperadas, por decirlo menos. Y en el mundo real, típico que es necesario definir objetos con multiples componentes, ¿Verdad? Es por ello que conviene usar un lenguaje que sea lo suficientemente compacto y en el cual no se pierda información en el proceso.
Como definición (muy informal), un vector en algún espacio Euclideano que vive en un espacio de $N$ dimensiones ${\displaystyle \mathbb {R}^{N}}$, puede ser descrito de la siguiente forma:
\[\begin{align} \mathbf{x}& = x_{1}\hat{e}_{1}+x_{2}\hat{e}_{2}+x_{3}\hat{e}_{3}+\cdots+x_{N}\hat{e}x_{N} \\ & = \sum_{i=1}^{N}x_{i} \hat{e}_{i} \\ \end{align}\]POR AHORA estaremos restringidos a vectores trimidensionales $\mathbf{x} = x \hat{i}+ y \hat{j}+z \hat{k}=(x,y,z)$.
Teoría de la relatividad General, de Bert Janssen. LINK
Electrodinámica, de Guillermo Rubilar. LINK
Wikipedia: Iré recolectando los links desde dónde tome información, y la iré dejando acá abajo.
Einstein’s steady-state theory: an abandoned model of the cosmos Parte de la bibliografía sugerida para este curso
Publicadas en 1865, James Clerk Maxwell (1832-1879) compiló el trabajo de Charles Coulomb, André-Marie Ampère, felix Savart, Jean-Baptiste Biot Michael Faraday y Hans Christian Orsted. Condensó en 4 expresiones (ya sean de forma diferencial y/o integral), las cuales tienen la siguiente forma:
| Ley de Gauss para el campo eléctrico | $ \displaystyle \nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$ |
| Ley de Gauss para el campo magnético | $ \displaystyle \nabla \cdot \mathbf{B} = 0 $ |
| Ley de inducción de Faraday | $ \displaystyle \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} $ |
| Ley de Ampere-Maxwell | $ \displaystyle \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} $ |
donde:
Si consideramos las leyes de Maxwell en el vacío, no existirán ni cargas $\rho$ ni corrientes $\mathbf{J}$ que puedan modificar actívamente los campos $\mathbf{E}$ y $\mathbf{B}$, por lo que las ecuaciones anteriores se reducen a:
| Ley de Gauss para el campo eléctrico | $ \displaystyle \nabla \cdot \mathbf{E} = 0$ |
| Ley de Gauss para el campo magnético | $ \displaystyle \nabla \cdot \mathbf{B} = 0 $ |
| Ley de inducción de Faraday | $ \displaystyle \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} $ |
| Ley de Ampere-Maxwell | $ \displaystyle \nabla \times \mathbf{B} = \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} $ |
Así, considerando una de las clásicas identidades vectoriales para un campo vectorial en tres dimensiones espaciales $\mathbf{A}(\mathbf{x}) = \mathbf{A}(x,y,z)$:
\[\nabla \times \left( \nabla \times \mathbf{A} \right) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A},\]donde $\nabla^2$ es el operador Laplaciano (la divergencia del gradiente $\nabla \cdot \nabla $).
Entonces, manipularemos las ecuaciones en el vacío y usaremos la identidad vectorial antes descrita. Si calculamos el rotacional de la Ley de Faraday, tenemos que:
\[\nabla \times \left( \nabla \times \mathbf{E} \right) = \nabla \times \left(-\frac{\partial \mathbf{B}}{\partial t} \right).\]La parte de la izquierda es igual a la parte de la izquierda de la identidad, por lo que podemos reemplazar:
\[\nabla (\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} = -\nabla \times \left(\frac{\partial \mathbf{B}}{\partial t} \right).\]Considerando que $\nabla \cdot \mathbf{E} = 0$ (¡El vacío!), tenemos que:
\[\nabla^2 \mathbf{E} = \nabla \times \left(\frac{\partial \mathbf{B}}{\partial t} \right).\]También, debemos tener en cuenta que las derivadas espaciales (representadas por $\nabla$) y las temporales ($\frac{\partial}{\partial t}$) no se afectan mutuamente, por lo que su orden es intercambiable, es decir: $\nabla \times \left(\frac{\partial \mathbf{B}}{\partial t} \right) = \frac{\partial}{\partial t} (\nabla \times \mathbf{B})$. Por lo tanto:
\[\nabla^2 \mathbf{E} = \frac{\partial}{\partial t} (\nabla \times \mathbf{B}).\]Finalmente, como $\nabla \times \mathbf{B} = \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$, llegamos a la ecuación:
\[\nabla^2 \mathbf{E} = \frac{\partial}{\partial t} \left( \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right).\]Reordenando los términos:
\[\nabla^2 \mathbf{E} - \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0,\]que es la ecuación de onda para el campo eléctrico $\mathbf{E}$ en el vacío. Para obtener la ecuación de onda del campo magnético $\mathbf{B}$ es análogo al anterior (tomar el rotacioal, aplicar la identidad, intercambiar derivadas, reemplazar el rotacional dentro de la derivada temporal, reordenar términos), por lo que obtenemos:
\[\nabla^2 \mathbf{B} - \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{B}}{\partial t^2} = 0.\]Ambas ecuaciones describen porciones de campo que viajan a través del vacío, a una velocidad finita v:
\[v = \frac{1}{\sqrt{\mu_0 \varepsilon_0}} = c \sim 3 \times 10^{8} \frac{[\mbox{m}]}{[\mbox{s}]},\]la que es nada más ni nada menos que la velocidad de la luz. Por lo tanto, Un cambio en el campo electromagnético genera por lo tanto más cambios, resultando en paquetes de campo propagándose por el espacio independientemente de cargas y corrientes. Estos paquetes de campo se llaman ondas electromagnéticas.
Pero: las ondas viajan con velocidad c ¿Con respecto a qué?
Sistema de referencia inercial (SRI): En mecánica Newtoniana, un SRI es un sistema donde las leyes de movimiento cumplen las leyes de Newton, tal que:
\[\frac{d}{dt}(\mathbf{p}) - \mathbf{F}_{\mbox{reales}} = 0,\]donde $\mathbf{p} = m \mathbf{v}$ es el momentum lineal de cierta partícula en movimiento. En un sistema no inercial, tenemos que:
\[\frac{d}{dt}(\mathbf{p}) - \mathbf{F}_{\mbox{reales}} - \mathbf{f}_{\mbox{ficticias}} = 0,\]En este contexto: ¿qué significaría una fuerza ficticia? ¿Qué ejemplos se conocen de $\mathbf{f}_{\mbox{ficticias}}$?
Algunas observaciones sobre los SRI:
Para relacionar un sistema inercian en movimiento rectilineo uniforme y uno estático, se utilizan las transformaciones de galileo, esquematizado en la siguiente imagen:
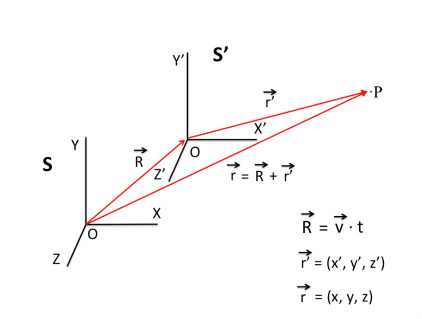
Figura 1: esquema de la relatividad de Galileo, imagen tomada desde este link
Para describir la posición de un punto $P$ cualquiera en el espacio desde el origen de coordenadas $O$, se considera el vector $\mathbf{r}=x \hat{i}+ y \hat{j}+z \hat{k}$. También podemos considerar otro sistema de coordenadas que, a un instante $t$, describe el mismo punto $P$ desde el origen $O’$, usando el vector $\mathbf{r}’=x’ \hat{i}+ y’ \hat{j}+z’ \hat{k}$. Si el sistema $O’$ se desplaza a una velocidad constante $\mathbf{V}$ con respecto al observador $O$, en cierto instante $t$, el vector que describe la posición del observador $O’$ desde $O$, será $\mathbf{R} = \mathbf{V} \cdot t$.
Por las propiedades de suma de vectores, tenemos que:
\[\mathbf{r} = \mathbf{r}' + \mathbf{R} = \mathbf{r}' + \mathbf{V} \cdot t.\]Escribiendo la igualdad anterior término a término, tenemos que:
\[\begin{align} x \hat{i}+ y \hat{j}+z \hat{k} =& x' \hat{i}+ y' \hat{j}+z' \hat{k} + \mathbf{V} \cdot t \\ =& x' \hat{i}+ y' \hat{j}+z' \hat{k} + V_x t\ \hat{i} + V_y t\ \hat{j} + V_z t\ \hat{k} \\ =& (x'+V_x t)\hat{i} + (y'+V_y t)\hat{j} + (z'+V_z t)\hat{k} \\ \end{align}\]Por lo tanto, tenemos expresiones para cada coordenada:
| $x= x’+V_x t$ | $x’= x-V_x t$ |
| $y= y’+V_y t$ | $y’= y-V_y t$ |
| $z= z’+V_z t$ | $z’= z-V_z t$ |
Las transformaciones de Galileo para cada coordenada se pueden utilizar para obtener la velocidad y la aceleración del sistema dinámico descrito anteriormente. Por ejemplo, consideremos el origen $O’$ que se mueve con velocidad constante $\mathbf{V}_c$ y descrito por el vector $\mathbf{r}’=\mathbf{r} - \mathbf{V}_c \cdot t$. Si quisiéramos obtener la velocidad del sistema:
\[\mathbf{v}' =\frac{d \mathbf{r}'}{dt} = \frac{d}{dt}(\mathbf{r} - \mathbf{V}_c \cdot t) = \mathbf{v} - \mathbf{V}_c,\]Así, tenemos el resultado:
\[\mathbf{v}' = \mathbf{v} - \mathbf{V}_c.\]De forma análoga, alguien podría estar interesado en la aceleración del sistema, por lo que sólo queda derivar temporalmente nuevamente:
\[\mathbf{a}' = \frac{d \mathbf{v}'}{dt} = \frac{d}{dt}(\mathbf{v} - \mathbf{V}_c) = \mathbf{a},\]Por lo tanto:
\[\mathbf{a}' = \mathbf{a}.\]Como se observa de la última ecuación, todos los sistemas de referencia inerciales miden la misma aceleración. Un resultado simple, pero poderoso: ¿Cuál es la gran conclusión que podemos obtener desde aquí? Tiene que ver con los privilegios.
Las velocidades son relativas, pero las aceleraciones son absolutas. Entonces cuando apacere una velocidad, también hay que preguntarse: velocidad: ¿Con respecto a qué sistema de referencia?. Entonces, de forma cualitiva, el principio de la relatividad de Galileo se expresa de la siguiente manera:
| Es imposible determinar a base de experimentos (mecánicos (o sea que soltando bolitas o con planos inclinados)) si un sistema de referencia está en reposo o en movimiento uniforme y rectilineo. |
A continuación presento algunos videos que visualizan el concepto de la velocidad relativa.
los cazadores de mitos: Sistema cañon-CamionetaLink
Visualización de la inercia en diferentes lanzamientos de pelotasLink, observar que en último caso (cuando la masa decrece) no se cumple el comportamiento esperado: ¿Por qué?
Top secret: escena del trenLink
Resumiendo, lo que nos dice Galileo es que hay cantidades que son relativas para diferentes SRI (como la velocidad, por ej) y hay otras cantidades absolutas, como lo es la Aceleración. Además, la teoría Electrodinámica de Maxwell predice ondas electromagnéticas que se propagan a la velocidad de la luz $c$. Pero ¿se propagan a una velocidad $c$ con respecto a qué?. Ésta es la pregunta fundamental de la relatividad especial.
Hasta ese momento, las ondas electromagnéticas necesitaban un medio para propagarse, por ende las ondas se propagarían a la velocidad de la luz con respecto al SRI co-movil con ese medio. Era una buena solución y el medio fue llamado el éter.
Entonces, dada la lógica Newtoniana de suma de velocidades, un observador que se mueve con una velocidad $v$ con respecto al éter tendrá que medir entonces que la luz se propaga (dependiendo si se acerca o se aleja) a la velocidad:
\[c' + c \pm v,\]si asumimos que el observador se mueve en la misma dirección que una onda Electromagnética, verá que la onda está estática ($c’=0$) ya que se encontraría en reposo con respecto al observador.
El hecho anterior es, en general, incompatible con la teoría electromagnética. El único escenario que las leyes de Maxwell admiten soluciones de campo estáticas es que explícitamente los campos $E$ y $B$ sean constantes con respecto al tiempo, tal que $\frac{\partial}{\partial t}\mathbf{E} = \mathbf{0}$ o $\frac{\partial}{\partial t}\mathbf{B} = \mathbf{0}$.
Algo debía estar mal, y debían seguir proponiendo qué era.
Otra pieza de información surgió desde el llamado experimento de Michelson-Morley, los cuales usaron “el interferómetro” para medir la velocidad de la luz con respecto al éter. Dicho sea de paso, la invención del interferómetro les valió el premino novel de físíca del año ().
Como la luz es una onda, los posibles efectos de la interferencia deberían ser apreciables. Entonces, se hace interferir un haz de luz complétamente caracterizado consigo mismo, haciendo que se divida en un “divisor de haces”, viajen haciéndolos rebotar en espejos diferentes, y luego viajen de vuelta hacia una pantalla donde será distinguible el patrón de interferencia.
Si definimos nuestro SRI en la tierra, podríamos considerar que la tierra se mueve a una velocidad $v$ con respecto al éter. El interferómetro comparte el SRI de la tierra, y en un isntante se emite un haz de luz que recorre el interferómetro y vuelve a la pantalla. Se espera que los caminos de estos haces sean modificados por la suma de velocidades en los diferentes caminos que toma el haz, por ende, exista un patrón de interferencia detectable en la pantalla.
El resultado fue controversial: con la resolución instrumental del momento se esperaba medir un valor de desfase $\Delta \Phi$, pero tal desfase no se encontró. Se probó el experimento en muchos contextos diferentes y nunca hubo resultado.
El físico irlandés George FitzGerald (1851-1901) encontró una forma de conciliar la situación, sugiriendo que cualquier objeto que tiene una velocidad $v$ con respecto al éter disminuyen en longuitud en un factor de $\sqrt{1-\frac{v^2}{c^2}}$. Por lo tanto:
\[\displaystyle L'=L\sqrt{1-\frac{v^2}{c^2}},\]Donde $L’$ es la longitud del cuerpo que se mueve, en la dirección del movimiento; y L es la longitud que debería tener en el reposo. En condiciones normales, el valor de esta corrección de longitud es muy pequeño. Por ejemplo, si un cuerpo se desplazara con un 10% de la velocidad de la luz (o sea, 30.000 [km/s]), su longitud se contrae ligeramente:
\[\begin{align} \displaystyle L' =& L\sqrt{1-\frac{v^2}{c^2}} \\ =& L\sqrt{1-\frac{(0.1c)^2}{c^2}}\\ =& L\sqrt{1-0.01}\\ =& L\sqrt{0.99}\\ \end{align}\]¿A qué velocidad se contraerá un objeto hasta alcanzar la mitad de la longitud que tiene en reposo? Respuesta: $v=0.866 c$.
¿Qué ocurre con la longitud de un cuerpo que se mueve a una velocidad igual a la luz?
Casi en paralelo, Hendrik Anton Lorentz (1853-1928) trabajó en el problema de forma independiente, reproduciendo las observaciones de FitzGerald y estableció que las leyes de Maxwell son invariantes bajo las siguientes transormaciones, si asumimos una velocidad de movimiento $v$ en el eje coordenado x:
\[\begin{align*} x' &= \gamma (x - vt) \\ t' &= \gamma \left( t - \frac{vx}{c^2} \right) \end{align*}\]donde el factor $\displaystyle \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$ es el llamado factor de Lorentz, en cual tiene a 1 cuando la velocidad $v$ es pequeña, en comparación a la velocidad de la luz $c$. Dicho de otra forma, en el límite donde la razón $v/c \to 0$ es:
\[\lim_{ \frac{v}{c} \to 0} \gamma = \lim_{ \frac{v}{c} \to 0} \frac{1}{\sqrt{1}} = 1,\]esta es la razón de que los efectos relativistas son indetectables por nuestros sentidos en velocidades “newtonianas” (velocidades $v$ pequeñas en comparación a la velocidad de la luz $c$), por eso las transformadas de Lorentz tiende a las transformaciones de galileo.
El razonamiento forma de obtener las transformaciones de Lorentz fue la siguiente:

Figura 2: esquema de la relatividad de Galileo, imagen tomada desde
Supongamos que dos observadores $O$ y $O’$ definen sus sistemas de coordenadas tal que, en el instante $t=t’=0$, los origenes coinciden. Entonces, en el instante $t=0$, se emitirá un pulso electromagnético que se alejará a la velocidad de la luz $ct$ de forma esférica, y el observador se empieza a mover hacia la derecha a velocidad constante $v$.
La transformación lineal más general entre los sistemas $(x,y)$ e $(x’,t’)$ será de la forma:
\[\begin{align*} x' &= Ax + Bt \\ t' &= Cx + Dt \end{align*}\]donde los coeficientes $A,B,C,D$ son funciones de $v$ y $c$. Como en cáda momento se cumple la condición $x=0$, podemos reducir lo anterior a:
\[\begin{align*} x' &= Bt \\ t' &= Dt \end{align*}\]si consideramos que $dx’ = B dt$ y que también $dt’ = D dt$, tenemos que:
\[-v = \frac{dx'}{dt'}=\frac{B}{D},\]donde el signo negativo es porque el observador $O’$ se mueve hacia la derecha. Otro hecho que se puede usar es que en el origen de coordenadas de $O’$, siempre está en reposo con respecto a si mismo, por lo tanto $x’=0$, así:
\[0 = Ax + Bt\]Si derivamos con respeto a $t$, tenemos que
\[0 = Av + B \Rightarrow B = -v A\]Con estos hechos reducimos nuestras ecuaciones iniciales a:
\[\begin{align*} x' &= A(x - vt) \\ t' &= A \left( \frac{C}{A}x + t \right) \end{align*}\]Además, si consideramos que en el momento $t=t’=0$, cuando se emite el pulso electromagnético. Después de un tiempo, el observador $O$ tendrá unas coordenadas que satisfacen una esfera, de la forma:
\[x^2 + y^2 + z^2 =(ct)^2.\]Pero para $O’$, el pulso también se expande como una esfera, por lo tanto:
\[x'^2 + y'^2 + z'^2 = (c t')^2\]La condición para que cada sistema funcione es que:
\[(ct)^2 - x^2 = (ct')^2 - x'^2\]Haciendo álgebra podemos llegar a que:
\[A = \frac{1}{\sqrt{1-v^2/c^2}} = \gamma \\ C = \frac{-v/c^2}{\sqrt{1-v^2/c^2}} = -\frac{-v \gamma}{c^2}\]y con eso se logran demostrar las transformaciones de Lorentz. Observe que las transformaciones están construidas tales que la cantidad
\[s^2 = (ct)^2 - x^2 - y^2 - z^2 = (c t')^2 - x'^2 - y'^2 - z'^2\]se mantenga “invariante”. La cantidad $s^2$ es conocido como intervalo, métrica. Básicamente es el valor al que está asociada la distancia en cierto intervalo:
\[ds^2 = dx^2 - c^2 dt^2\]En este sentido, este intervalo es una magnitud absoluta de la relativdad especial. Posee el mismo valor en todos los sistemas inerciales. $ds^2$ es una especie de distancia en el espacio-tiempo 4-dimensional: el espacio de Minkowski. Por ejemplo si un suceso ocurre en $(ct_1,x_1,y_1,z_1)$, y otro en $(ct_2,x_2,y_2,z_2)$, la cantidad:
\[\Delta s^2 = (x_2 - x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2 - c^2(t_2 - t_1)^2\]es el cuadrado de la distancia de esos dos sucesos.
El principio de la relatividad segun Einstein:
| Las leyes de la física deben tener la misma forma en todos los sistemas de refencias inerciales. |
El principio de la constancia de la luz:
| La velocidad de la luz en el vacío es igual para todos los observadores u tiene el valor de 299.792,458 [km/s], independientemente del estado de movimiento de la fuente. |
El vector de posición, radio vector o simplemente Vector posición $\vec{r}$ es aquel vector que parte desde el origen de algún sistema coordenado hasta un punto de interés $P$. Muy útil en física para describir algún punto de vista particular o sistema de referencia. Por esta misma razón es que otra persona podría definir su propio sistema coordenado (o punto de vista) y describir la realidad de otra forma. Ambas descripciones deberían ser equivalentes asumiendo que existe una realidad física objetiva. Considere una escala de tiempo igual para todos los sistemas de referencia.
Si ambos sistemas de referencia observan una particula moverse desde un punto inicial $P_i$ a otra posición final $P_f$:
En la mecánica Newtoniana aparecen dos tipos de masas diferentes, con propiedades bastante diferentes para el fenómeno que cuantificaban.
Un elemento de línea o elemento de longitud, de forma muy simplificada, es el desplazamiento infinitesimal de un vector definido sobre cierto espácio métrico. Por lo tanto, (e informalmente) la raiz cuadrada de $ds^2$ será el cuadrado de la longitud de un desplazamiento infinitesimal dentro de cierto espacio vectorial. Definido de esa forma, la longitud $s$ de una curva parametrizada bajo una cantidad $\lambda$ será calculada de la forma usual $s = \int_{\lambda_1}^{\lambda_2} \sqrt{|ds^2|} d\lambda.$
Hallar el cuadrado del elemento de línea en coordenadas cilíndricas.
\[\begin{align*} x &= \rho \cos(\phi) \\ y &= \rho \sin(\phi) \\ z &= z \\ \end{align*}\]Consideremos el siguiente vector de tres dimensiones:
\[\vec{x}(x,y,z) = x \hat{i}+ y \hat{j}+z \hat{k},\]que es el vector que describe cualquier punto en el espacio de tres dimensiones euclidieano. Entonces, considerando el cambio de variable propuesto por las coordenadas cilíndricas, podemos escribir el vector de la forma:
\[\vec{x}(\rho,\phi,z) = \rho \cos(\phi) \hat{i}+ \rho \sin(\phi) \hat{j}+z \hat{k}.\]Para obtener el elemento de línea de estas coordenadas, diferenciamos el vector con respecto a sus variables:
\[\begin{align*} d\vec{x} &= \dfrac{\partial \vec{x}}{\partial \rho} d\rho + \dfrac{\partial \vec{x}}{\partial \phi} d\phi + \dfrac{\partial \vec{x}}{\partial z} dz \\ &= d\rho(\cos(\phi) \hat{i} +\sin(\phi) \hat{j}) + d\phi(-\rho\sin(\phi)\hat{i}+\rho\cos(\phi)\hat{j}) + dz \hat{k} \\ &= d\rho \hat{\rho} + \rho d\phi \hat{\phi} + dz \hat{k} \\ \end{align*}\]donde hemos definido las cantidades $\hat{\rho}= \cos(\phi) \hat{i} +\sin(\phi) \hat{j}$ y $\hat{\phi} = -\sin(\phi)\hat{i}+\cos(\phi)\hat{j}$. Entonces, el cuadrado del elemento de línea ds^2 será:
\[d\vec{x}\cdot d\vec{x} = ds^2 = d\rho^2 + \rho^2 d\phi^2 + dz^2\]Considerando las transformaciones de Lorentz a lo largo del eje $x$ en la dirección $\hat{i}$, las ecuaciones quedan de la forma:
\[\begin{align*} x' &= \frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (x-vt) \\ y' &= y \\ z' &= z \\ t' &= \frac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} = \gamma (t-\frac{vx}{c^2}) \\ \end{align*}\]Entonces,
\[\begin{align*} \Delta s^2 &= c^2 \Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 = (c \Delta t')^2 - (\Delta x')^2 - (\Delta y')^2 - (\Delta z')^2 \\ &= c^2 \Delta t^2 - \Delta x^2 = (c \Delta t')^2 - (\Delta x')^2 \end{align*}\]Por lo tanto, como tenemos expresiones que relacionan ambos sistemas de refencia, tenemos que:
\[\begin{align*} c^2 \Delta t^2 - \Delta x^2 &= (c \Delta t')^2 - (\Delta x')^2 \\ &= c^2 \gamma^2 \left(\Delta t-\frac{v\Delta x}{c^2} \right)^2 - \gamma^2 \left( \Delta x-v \Delta t \right)^2 \\ &= c^2 \gamma^2 \left( \Delta t^2 - \frac{2v}{c^2} \Delta t \Delta x + \frac{v^2}{c^4}\Delta x^2 \right) - \gamma^2 \left( \Delta x^2 -2v \Delta x \Delta t + v^2 \Delta t^2 \right) \\ &= c^2 \gamma^2 \Delta t^2 + \frac{v^2}{c^2} \gamma^2 \Delta x^2 - \gamma^2 \Delta x^2 - \gamma^2 v^2 \Delta t^2\\ &= c^2 \gamma^2 \Delta t^2 \left( 1-\frac{v^2}{c^2} \right) - \gamma^2 \Delta x^2 \left( 1-\frac{v^2}{c^2} \right) \\ &= c^2 \Delta t^2 - \Delta x^2, \\ \end{align*}\]Que era lo que queríamos demostrar.
Sobre didactica de la fisica https://www.matematicasenaccion.unican.es/transparencias20112012/CuadrivectoresMNDFisica.pdf
Transformaciones de Lorentz en coordenadas no-euclideanas. https://ejournal2.undip.ac.id/index.php/jpa/article/view/4951/2777
Tarea 2:
1.- Considere dos sistemas de referencia inerciales: $O$ y $O’$, donde $O’$ se mueve a velocidad constante $v$ en la dirección $\hat{k}$ con respecto a $O$. Demuestre que las transformaciones de Lorentz entre estos sistemas inerciales dejan invariante la metrica espacio-temporal.
2.- Si el sistema de referencia $O’$ a velocidad $v$ observa un objeto con longitud $L’$: ¿Cuál será la longitud que verá el observador en el sistema $O$? ¿Qué velocidad debe tener $O’$ para que observe la mitad de la longitud que observa $O$?
3.- En el contexto newtoniano, derive la ecuación de movimiento (ecuación itinerario) correspondiente a una partícula dentro de un campo gravitatorio uniformemente acelerado, en función de la masa inercial y la masa gravitatoria. Describa cómo el principio de equivalencia local resuelve la discrepancia conceptual masa gravitatoria/masa inercial. Discuta cualquier aspecto que considere relevante.